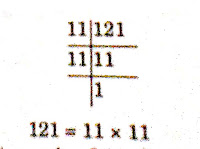NCERT Solutions for Class 8 Maths Chapter 4

           Multiplication and Division of Algebraic expressions

Points to remember

• While multiplying variable, exponential law is followed.
• To divide a polynomial it is convenient to divide each term of the polynomial by the monomial.
• (a + b) (c + d) = a(c + d) + b(c + d)

                              = ac + ad + bc + bd

• The process of division is continued till the exponent of the divisor does not become less than the exponent of the remainder for the algebraic expression.

Exercise 4.1

https://youtu.be/-BqfAVbTWmk

    Exercise 4.2

        

https://youtu.be/9nXpjsiaozs

Exercise 4.3

Q.1 Write the given polynomials in the decreasing order of their variables.

  

https://youtu.be/Nfot1hbZtjE

Q.2. Divide and say whether the division are multiple factor of the dividend.

(1). x²-11x+30 by (x-5)

(2). x²+20x+91 by x+7

(3). x²-5x-6 by x-6

(4). x³-5x²-2x+24 by x-4

(5). a²+2ab+b² by a+b

Q.3. Divide and prove that the divisor and the dividend are not multiple fators. write down the quotient and the reminder for the following expressions.

(1). x³ +2x²+ 3x +4  by x-1

(2). -12+3x² -4x+x³  by  x+5

(3). 4x⁴ – 2x³-10x²+13x-6  by  2x+3

(4). 8x³ -6x² +10x+15  by  4x+1

Q. 4 Divide and verify :

          Dividend = Divisor * Quotient + remainder

(1). m²-3m+7  by  m-2

(2). a³ – 2a² +a +2    by a+2

(3). 9x³ + 15x² - 5x + 3  by  3x+1

(4). 2x³ + 3x² + 7x + 15   by x² +4

for more help join my youtube classes 

cgbsemathssolutions

Read More

NCERT Solutions for Class 8 Maths Chapter 3

 NCERT Solutions for Class 8 Maths Chapter No. 3

PARALLEL LINES

Points to Remember

• Two or more lines in the same plane which do not intersect each other are called parallel lines.
• The perpendicular distance between two lines (parallel lines) is always the same.
• The perpendicular drawn at two points on the same line are parallel.
• When two straight lines are intersected by any inclined line, then the intersected part between the two straight line is known as the intersecting segment.
• The ratio o intercepts on parallel lines by two intersecting lines are equal
• The line joining the mid points of the two sides of a triangle is parallel to its third side.

Exercise 3.1

For this exercise we have the video solution which make you easy to understand the questions solution.

https://youtu.be/-BqfAVbTWmk

Exercise 3.2

https://youtu.be/-BqfAVbTWmk

Read More

Earn Money Online

EARN MONEY ONLINE

earnmoney.in.net

If you are looking to earn money fast and more at small time then join this scheme through me and earn money.
It's matter of 600 rupee only

Read More

Online security articles

ONLINE AND SECURE

We use the Internet on daily basis. With the help of the Internet the world is connected more than it has ever been. The Internet has now become the backbone of communication and an information resource for humankind.

CONCEPT OF CYBER SECURITY

Today, we have become dependent on the computers and the Internet to run our day to day lives. Our general needs of life like communicating with our loved ones, doing business, tracking financial status, shopping, paying utility bills, etc. are now done online with  the help of a computer and the Internet. Over the last couple of years, several applications and software have also evolved to run and exchange information o the web. People are creating newer and more innovative ways to cause harm to the average user on a computer. Cyber security is about protecting yourself and everyone else who are using the Internet and ensuring that they don't become the next victim.

• Confidentiality: This indicates that the information or the data that is typically meant for a defined set of people, is accessible to only that defined group. In case it is accessible outside or is made accessible to anyone outside the defined group, the confidentiality of that data/information is breached.
• Integrity:  This suggests that the information should be controlled against and unauthorized modification, at rest or in communication. If the information gets tampered with, it will indicate a breach i integrity.
• Availability:  This represents the availability of the resource, when required. In case it is not available at the time of requirement, this would indicate a breach of availability.

SECURITY RISKS (OFFLINE AND ONLINE)

                  Security risk is a term that defines and event or action that could be harmful for a computer hardware, software, data information or its processing capability Some breaches to computer security are planned and some are accidental, however, they can still have a grave impact on the user/owner of the resource. These illegal acts performed through a computer are referred to as a computer crime. Any illegal act involving are generally referred to as cyber crime. 

                 Let's explore some forms of security breaches that are common in today's world.

• Ransomware:  People install programs/software i our machines using various techniques and then encrypt the complete content of your personal drives, files and folders. They then demand ransom(money) in exchange for providing you access to your content/data.
• Data Theft/Hacking : When people break in the computers or the computer networks to steal confidential information, it is known as data theft or hacking. Hackers are computer experts who break  into computer systems and networks. Hackers can be classified as, 'Blackkhat', 'Whitehat', and 'Greyhat' hackers. 
• Virus Dissemination: Viruses are computer software programs that install themselves onto any system that they access to. When a leads to a disruption in the computer operations and the corruption because once they infect one machine on the Internet, they can use this as the base and infect other machines form the host. There are various kinds  of viruses and we will discuss them in details in another section.
• Spoofing:  Spoofing is an act of gaining unauthorized access to someone's computer to access someone's personal information. Intruder may steal someone's bank account details or passwords.
• Masquerade or Identity Theft: This is and act of accessing  a compute using hacked credentials or stealing the password of networks or administrator command functions to access more privileged part of the system/networks.
• Digital Snooping:   This is an act of electronic monitoring of the digital networks to uncover passwords or other sensitive data. Users or even system administrators have been found online at unusual or off-shift hours doing digital snooping. Hackers have now developed software like key-loggers that are active o a system in the background and not visible to the user; it silently captures each keystroke that is pressed on the system and then sends it back to their creator.
• Sabotage:  Disgruntled employees can create mischief and sabotage a computer system. Employees make up the group that is most familiar with their employer's computers and applications of the examples of computer-related employee sabotage include hostage, etc. Logic bombs are also used by some employees to automate such operations.
• Email Attacks:    Sending and receiving emails are the prime source for spreading computer viruses, malware, various sniffer programs, etc. Forms of email attacks, spamming and phishing have emerged as two security risk which have become quite popular in the past few years.
• Malware:  Malware is class of software that is created with malafide intentions. Malwares are well thought, well-designed and meticulously engineered with and intent to cause damage or to steal information form the victim's computer system. Malware is a very broad classification and it can be further divided into two sub categories:  Infectious Malware and Concealment Malware.

Virus (definition and types)

A Computer virus is a program that can multiply and spread itself from one computer system to another causing various types of damaging effects. It is a program or a piece of code that is loaded into the computer's memory without the user's knowledge and runs without the user's awareness. Viruses can also make copies or replicate themselves. However, computer viruses are man-made, making them different from the biological viruses. Even a simple virus can be dangerous as it ca make a copy of it over and over again. this will quickly use up the available memory and the other resources, bringing the system to a stop. A virus can be more dangerous if it is capable of transmitting itself across networks and bypassing security systems. There are myriads of viruses that exist today and many more being added into the cyberspace everyday. A virus is spread by the infected floppy disks, Universal Serial Bus (USB), or the Internet etc. Some of the more common types of viruses are as follows:

• Boot Sector Virus:  This category of viruses infect the boot sector of the disks forcing them to loose data and in some cases, rendering them unusable altogether. 
•  Terminate and Stay Resident (TSR) Virus:  These viruses, once loaded into the memory of the infected computer, remain stationed into the memory and infect any healthy disk used subsequently. 
• Application Software Virus: These viruses infect the application programs, such as Microsoft word and use them for propagation as well. Macro virus were one such example of these.
• Time/Logic Bomb:  A time/logic bomb is a virus or worm designed to activate at a certain date/time or when a specific condition is true and not immediately at the time of infection. Y2k or Year 2000 virus belonged to this category. It badly damaged the computer system at 00:00:01 am on the 18 Jan 2000 all over the world sending the cyber world into panic.

Online security

Trojan, Rootkits, Keylogger, Worms

A computer on a network is accessed by many uses. Files  are shared between these users and computer  on  a network. This makes a computer and the network vulnerable to attacks by viruses because of the underlying network. Let us discuss some of the common threats to the computers.

• Trojan:  A computer program that appears to be a useful software but actually causes damage, once installed or executed o the computer system is known as Trojan horse . This is the program that does more than its published specifications.
• Rootkits: A rootkit is a malicious software which hides  the programs form the normal methods of detection and enables continued privileged access to a computer.
• Keylogger: As the Internet grows rapidly, new kinds of security threats are reported on a daily basis. the Keylogger is a well known malware that can be built into Trojan horse and used to steal personal information.

Safety Issues for Teenagers on the Internet

At any moment of time, millions of users are online: at home, at school, at a friend's house, almost  everywhere. Most people online engage in activities like emailing, browsing, instant messaging, visiting social networking sites while working on the Internet. All these activities are very popular and fun but also need one to be careful. 

•  Online Dangers through emails:
• Online Dangers through Blogs:
• Online dangers through Chatting:
• Online dangers through Websites:

Read More

NCERT Solutions for Class 8 Maths Chapter 2

 NCERT Solutions for Class 8 Maths Chapter No. 2

EXPONENTS

• Chapter No. 2.    EXPONENT

INTRODUCTION

• When a is a number then a × a × a × ……….×….(n times) then the product is    where 'n' is called exponent and 'a' is called base.
• Some formulas:  

            (1)        a^m × aⁿ    =  a^m+n

(2)       a^m ÷ aⁿ  = a^m-n

(3)       (a^m)ⁿ        =  a^m×n

(4)       (ab)ⁿ        =  aⁿ  × bⁿ

(5)        aⁿ              =  1/(a-n)

            (6)        a⁰             = 1

(7)   (-1)^{Even no.} =1

(8)   (-1)^{Odd no.} = -1

(9)            (-a)^m  = {(-1) × a}^m = (-1)^m  × a^m

So,  (-a)^m  is positive or negative depends on (-1)^m  

If p and q is a rational number then

                                               

                                  [p\q]^m  = p^m \ q^m and [p\q]^-m = [q\p]^m

Exercise 2.1

Q.1.  Simplify the following :
(a)   (-5)³  
Sol:-         (-5)³     = {(-1) × 5}³

                            = (-1)³ × 5³

                            = (-1) × (5 × 5 × 5)

                            = -125      Ans.

(b).   (-4)⁵  

Sol:-           (-4)⁵   = {(-1) × 4}⁵

                            = (-1)⁵ × 4⁵

                            = (-1) × ( 4 × 4 × 4 × 4 × 4)

                            = -1024           Ans.
(c).   (-2)^6  
Sol:-             (-2)⁶   = {(-1) x 2}⁶

                                 = (-1)⁶ × 2⁶

                                 = 1 × (2 × 2 × 2 × 2 × 2 × 2)

                            = 64           Ans. 

(d).  (-3) ⁶ 

Sol:-          (-3) ⁶  =   {(-1) x 3}⁶

                             =    (-1)⁶ x 3⁶

                                 =     (1) x ( 3 x 3 x 3 x 3 x 3 x 3 )

                                 = 729         Ans.  

Q.2.   Write the following in the form of exponents.  :

(a).   5⁴ x (-5)²

Sol:-   5⁴ x (-5)² = 5⁴ x {(-1) x 5}²

                           = 5⁴ x (-1)²  x 5 ²

                           = (-1) ²  x 5⁴ x 5²

                           = 1 x 5^{4 +2}

                           =  1 x 5⁶

                           = 5⁶         Ans.

(b).   15 × (-15)²⁵

Sol:-    15 × (-15)²⁵ = 15 × {(-1) × 25 }²⁵

                                = 15 × (-1)²⁵  × (15)²⁵

                                = (-1)²⁵ × 15 × 15²⁶

                                = -1 × 15¹⁺²⁵

                                = -1 × 15²⁶

                                = -(15)²⁶                Ans.

(c).   12⁵ ÷ (-12)³ 

Sol:-   12⁵ ÷ (-12)³ = 12⁵/ (-12)³

                        = 12⁵ / {(-1×12}³

                    =  12⁵ / (-1)³ × 12³

                    = 12⁵/ -1 × 12³

                        = -12^5-3

                        = -(12)²          Ans.

(d).   (-p)¹⁴ ÷ (-p)⁷

Sol:-      (-p)¹⁴ ÷ (-p)⁷ = (-p)¹⁴/ (-p)⁷

                            = {(-1) × p}¹⁴ / {(-1) × p}⁷

                        = (-1)¹⁴ × p¹⁴/ (-1)⁷ × p⁷

                        =  -1 × p^14-7

                        =  -1 × p⁷

                        =-(p)⁷            Ans.

Q.3.    Verify the given statements by giving both the sides.

(a).   (-2)⁴ ×  (-2)²   = (-2)⁸  ÷ (-2)²

Sol:-   L.H.S.  (-2)⁴ ×  (-2)²   = {(-1) ×2}⁴ × {(-1) × 2}²

                                               =  (-1)⁴ × 2⁴  × (-1)² ×2²

                                               = 1   × 2⁴ × 1 × 2²

                                               = 2⁴ × 2²

                                               = 2⁴⁺²

                                               = 2⁶

R.H.S.     (-2)⁸  ÷ (-2)²          =  (-2)⁸ / (-2)²

                                                        =  {(-1) × 2}⁸ / {(-1) ×2}²

                                               =  (-1)⁸ × 2⁸ / (-1)² × 2²

                                               =  1 × 2⁸ / 1 × 2²

                                               = 2⁸ /  2²  = 2^8-2   =2⁶

                                Hence,  L.H.S.  =  R.H.S.

(b).  (-3)² × (-3)^-6 = 1 / (3²)²

Sol:-   L.H.S.   (-3)² × (-3)^-6 = (-3)² × 1 / (-3)⁶

                                     = (-3)²  /  (-3)⁶

                                     = {(-1) × 3}²  /  {(-1) × 3}⁶

                                     = (-1)²× 3²  /  (-1)⁶  × 3⁶

                                     = 1 × 3²  /  1 × 3⁶

                                     = 3² /  3⁶

                                     = 3^2-6

                                    = 3^-4

R.H.S.    1 / (3²)²       = 1 / 3^2×2+

                                   = 1 / 3⁴

                                  = 3^-4

                   Hence,    L.H.S.  = R.H.S. 

(c).  (-7)³²  ÷  (-7)³² = 1

Sol:-  L.H.S.   (-7)³²  ÷  (-7)³² = (-7)³²  /  (-7)³²

                                                 = {(-1) × 7}³²  /  {(-1) × 7}³²

                                                 = (-1)³² × 7³²   /   (-1)³² × 7³²

                                                 = 1 × 7³²  /  1 × 7³²

                                                 = 7³² / 7³²

                                                 = 7^32-32

                                                 = 7⁰

                                                 =  1  R.H.S.

    Hence,  L.H.S = R.H.S. 

Exercise 2.2

Q.1.  Simplify the following : 

(a).  (2/7)³ (1/2)³
Sol:-        (2/7)³  × (1/2)³ = (2)³ / (7)³  × (1)³ / (2)³

                                         = (2)³ / (2)³  ×  1 / (7)³

                                         = (2)^3-3 × 1 / 7 × 7 × 7

                                          = (2)⁰  × 1 / 343

                                          = 1 × 1 / 343 =  1/343     Ans.

(b).    (4/5)⁴  × (5/4)²

Sol:-          (4/5)⁴  × (5/4)² = (4/5)⁴  × (4/5)^-2

                                           = (4/5)^4+(-2)

                                                   = (4/5)^4-2

                                            = (4/5)²

                                           = 16/25                 Ans.

(c).   (-5)³÷(-1/5)²

 Sol:-       (-5)³÷(-1/5)²       =    (-5)³ ÷ (-1 × 5^-1)²

                                            =   (-5)³ ÷ (-1)² × (5^-1)²

                                            = (-5)³ /  1 × 5^-2

                                            = (-5)³  /  (5)^-2

                                            =  (-1)³ ×5³/ (5)^-2

                                            = -1 × 5³/ 5­^-2

                                            = -1 × 5^3-(-2)

                                                     = -1 × 5⁵

                                            = -3125                 Ans.

(d). (3/4)³×(3/4)^-5   

Sol:-     (3/4)³×(3/4)^-5         =  (3/4)^3+(-5)

                                            = (3/4)^3-5

                                             =(3/4)^-2

                                             = 1/(3/4)²

                                             = 1/ 9/16

                                             = 1 × 16/9

                                             = 16/9                   Ans.

Q. 2.  Express in the form of exponent :

(a).  -25/49

Sol:-                    -25/49      = (-1) × 25/49

                                            = (-1) × 5/7×5/7

                                            = (-1) × 5²/7²

                                            = (-1) × (5/7)²

                                            = -(5/7)²               Ans.

(b).   27/125

Sol:-                       27/125 = 3 × 3 × 3 / 5 × 5 × 5

                                           = 3³/5³

        =  (3/5)³                       Ans.

(c).  729/64

Sol:-                       729/64  =  (3 × 3 × 3  × 3 × 3 × 3)/ (2 × 2 × 2 × 2 × 2 × 2

                                            = 3⁶/ 2⁶

                                            = (3/2)⁶                 Ans.

Q. 3. Prove that  :

(a).   (5/7)⁷ × (7/5)⁷ – (3/19)² × (19/3)² = 0

Sol:-

         L.H.S.  (5/7)⁷ × (7/5)⁷ – (3/19)² × (19/3)² =  (5/7)⁷×(5/7)^-7 -  (3/19)² × (3/19)^-2

                                                                            =  (5/7)^7+(-7)    -  (3/19)^2+(-2)

                                                                            = (5/7)^7-7  -  (3/19)^2-2

                                                                            = (5/7)⁰   -  (3/19)⁰

                                                                            = 1-1

                                                                            = 0   R.H.S.

                                                           Hence,   L.H.S. = R.H.S.     Proved.

(b).  (p/q)^m  × (p/q)^m × (q/p)^m = (q/p)^-m

Sol:- 

            L.H.S.  (p/q)^m  ×   (p/q)^m × (q/p)^m

                                                                                = (q/p)^-m × (q/p)^-m  ×= (q/p)^m

                                                                   = (q/p)^-m+(-m)+m

                                                                  = (q/p)^-m-m+m

                                                                  = (q/p)^-m   R.H.S.

                                                        Hence,  R.H.S. = L.H.S.    Proved.

(c)  (25/16)^-4  = (16/25)⁴

Sol:- 

                          L.H.S.  (25/16)^-4         = 1/(25/16)⁴

                                                                        =   (16/25)⁴ R.H.S.

                                               Hence, L.H.S. = R.H.S.     Proved.

Q. 4.  Write True or False:

(a).  (-5/4)⁶⁵ = (-5)⁶⁵ / (4)⁶⁵

Ans.    True.

(b) (-32/19)¹⁵⁰  =  32¹⁵⁰ / 19¹⁵⁰

Ans.    True.

(c).  (25 × 3)⁵ = 25 × 3⁵

Ans.   False.

(d).  (27/16)^-15  = 27¹⁵/16¹⁵

Ans.      False.

                                

Read More

NCERT Solutions for Class 8 Maths Chapter 1

                                                           

NCERT Solutions for Class 8 Maths Chapter No. 1 

Square and Cube EXERCISE 1.1

• Chapter No. 1      SQUARE AND CUBES

INTRODUCTION

1.    If "n" is a number, then n × n or n² will be known as its square and n × n × n or  n³ will be called its 

        cube.

2.     Those numbers whose unit place have numbers like 2, 3, 4, or 8 cannot be perfect square numbers.

3.     If  a perfect square number ends in an even number of zeroes, then they would also be perfect squares.

4.    The squares and cubes of even numbers are always  even numbers and squares and cubes of odd 

        numbers are always odd numbers.

5.    The squares of any natural number "n" is the sum of the initial consecutive odd numbers.

6.     If three numbers are in such a sequence that the square of the greater number is equal t the sum of the         square of the remaining two numbers, then the numbers are known as Pythagoral Triplets e.g.   3² + 4² =  5²   therefore (3, 4, 5) make a Pythagoral Triplet.

7.      Square root is represented b the symbol "  √  ".  This is known as the symbol of under root or the

         square  root of the number. The number written under this symbol is determined.

                                              Exercise 1.1

Q.1. Pairs the multiple factors of the following number and say whether they are perfect squares or                not?
(1)      164
Sol:-

(2)     121

Sol:-

(3)      289

Sol:-   

          289 = 17*17

(4)     729

Sol:-

      

(5)     1100

Sol:-

Q.2.   Give reasons why the given numbers are not perfect squares.

(1)     12000

Sol:-  A perfect square never has odd number of zero in the end of the number, so 12000 is not a                    perfect square.

(2)     1227

Sol:-  The units digit of a perfect square is never 2, 3, 7 or 8, so 1227 is not a perfect square.

(3)     790

Sol:-  A perfect square never has odd number of zero in the end of the number, so 790 is not a                    perfect square.

(4)     1482

Sol:-  The unit digit of a perfect square is never 2, 3, 7 or 8, so 1482 is not a perfect square.

(5)     165000

Sol:-  A perfect square never has odd number of zero in the end of the number, so 165000 is not a                  perfect square.

(6)     15050

Sol:-   A perfect square never has odd number of zero in the end of the number, so 15050  is not a                  perfect square.

(7)     1078

Sol:-  The unit digit of a perfect square is never 2, 3, 7 or 8, so 1078  is not a  perfect square.

(8)     8123

Sol:-   The unit digit of a perfect square is never 2, 3, 7 or 8, so 8123  is not a  perfect square.

Q.3.   Find out the numbers whose squares are even numbers and whose squares are odd numbers?

Sol:- Since the square of even numbers are always even and square of odd number are always odd,               so  square of 14, 608, 11288, and 4010 are even numbers and square of 277, 179, 205, 1079,               1225, are odd numbers.

Q.4.   Look at the given pattern and fill in the blanks:-

                     

Sol:-      

                          

For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/    

                 

Exercise 1.2

Q.1.   Identify the perfect cubes in the given numbers.

(1)     125

Sol:-

125 is perfect cube.    Ans.

(2)     800
Sol:-

800 = 2*2*2*2*2*5*5

800 is not a perfect cube.      Ans.

(3)     729

Sol:-   

729 = 3*3*3*3*3*3


729 is a perfect cube.      Ans.


(4)      2744
Sol:-







2744 = 2*2*2*7*7*7



2744 is a perfect cube.       Ans.

(5)       22000
Sol:-








22000 = 2*2*2*2*5*5*5*11


22000 is not a perfect cube.    Ans.

(6)      832
Sol:-










     832 is not a perfect cube.    Ans.



Q.2.   Find out that smallest number which when multiplied by 256 will make the product a                  perfect cube.
Sol:-  Prime factors of 256.
       





256 = 2*2*2*2*2*2*2*2

Here, we get 2 triples of prime factors 2 but to get a third triple we will have to multiply once by 2.

 So, the given number should be multiplied by 2 to get a perfect cube.    Ans.



Q.3.   Find out the smallest number which when multiplied by 1352 will make the product a                  perfect cube.
Sol:-  Prime factor of 1352




Here in the factors of 1352, we get the triple of 2  but we do not get a triple of 13. So 1352 should be multiplied by 13. So that it become a perfect cube.                      Ans. 





Q.4.    Find out that smallest number which when multiplied by 8019 will make the quotient a                perfect  cube.
Sol:-   Prime factor of  8019
           





8019 = 3*3*3*3*3*3*11

Here in the factors of 8019, we get 2 triple of 3 but do not get a triple of  11 so that it becomes a perfect cube.             Ans.

For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/ 

Exercise 1.3

Q.1.     Find out the square root of the given numbers by prime factorization method.

(1)       361

Sol:-

Ans.

(2)       400

Sol:- 

Ans.

(3)      784

Sol:-  

Ans.

(4)      1024

Sol:- 

Ans.

(5)      2304

Sol:-

Ans.

(6)       7056

Sol:-

Ans.

Q.2.      A group of boys bought 256 mangoes and distributed it among themselves. If each boy                 got the number of mangoes equal to the number of boys in the group. Find out the                       number of boys in the group.

Sol:-     Let the number of boys in each group be x then each of x boys gets x mangoes.

             So total mangoes = x*x = x² 

             But total number of mangoes = 256

             So,      x²     = 256  

                                X² =2  × 2 × 2 × 2 × 2  × 2 × 2 × 2

              Taking square rot of the both sides

                √ x²=√2  × 2 × 2 × 2 × 2  × 2 × 2 × 2        (all numbers are in square rooot)

                   x =  2  × 2 × 2 × 2

                   x = 16

             So, the number of boys in each group are 16.          Ans.




For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/ 

Exercise 1.4

Q.1.    Find out the square root of following by division method.

(1)     529
Sol:-







23 is Ans.

(2)       1369
Sol:-







 37 is Ans.

(3)      1024
Sol:-

32 is Ans.


(4)      5776
Sol:-






76 is Ans.


(5)      900
Sol:-






30 is Ans.
(6)       7921
Sol:-

0 is Ans.

(7)        50625
Sol:-

225 is Ans.

(8)       363609
Sol:-











6703 is Ans.

Q.2.     In a cinema hall the owner wants to organize the chair in this way that the number of 

            rows and columns of seats should be equal. If there are total 1849 seats then find out the 

            numbers of rows and column.

Sol:-    Given that,

                              the total number of seats are 1849

                               Then, the number of columns and rows are

                                   1849 = 43*43

                       hence the number of rows and columns are 43              Ans.

Q.3.      The area of a square garden is 1444 square meter, so find out the length and breadth of 

             that garden.

Sol:-      Given that, 

                             the area of a square garden is 1444 sq.m.

                            then, the length and breadth of that garden will be

             we know that area of square is = L× L

                      so the length of the garden well be 

                                      1444 = 38 × 38             

                   Hence, the length and breadth of the garden is same 38 m.          Ans.

For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/ 

  Exercise 1.5

Q.1.       Find out the squares root of following numbers.

(1).        7.29

Sol:-        

Ans.

(2).       16.81
Sol:-








Ans.

(3).       9.3025
Sol:-










Ans.


Q.2.      Find out the squares root of following up to two places of decimal.

(1).     0.9
Sol:-










Ans.

(2).     5
Sol:-










Ans.

(3).     7
Sol:-










Ans.



For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/ 

Exercise 1.6

Determine the cube root of following.

(1).    125

Sol:-  

Ans.


(2)     343
Sol:-











Ans.

(3).     1331
Sol:-









Ans.



(5).     9261
Sol:-












Ans.

(6)    166375
Sol:-











Ans.

(7)      4913
Sol:-










Ans.

(8)     42875
Sol:-












Ans.



For more help visit : https://www.learncbse.in/ncert-solutions-for-class-8-maths/ 

WE HAVE LEARNT

1.    If "n" is a number, then n × n or n² will be known as its square and n × n × n or  n³ will be called its 

        cube.

2.     Those numbers whose unit place have numbers like 2, 3, 4, or 8 cannot be perfect square numbers.

3.     If  a perfect square number ends in an even number of zeroes, then they would also be perfect squares.

4.    The squares and cubes of even numbers are always  even numbers and squares and cubes of odd 

        numbers are always odd numbers.

5.    The squares of any natural number "n" is the sum of the initial consecutive odd numbers.

6.     If three numbers are in such a sequence that the square of the greater number is equal t the sum of the          square of the remaining two numbers, then the numbers are known as Pythagoral Triplets e.g.                             3² + 4² = 5²   therefore (3, 4, 5) make a Pythagoral Triplet.

7.      Square root is represented b the symbol "  √  ".  This is known as the symbol of under root or the

         square  root of the number. The number written under this symbol is determined.

Read More